Communication topology

Supported topologies

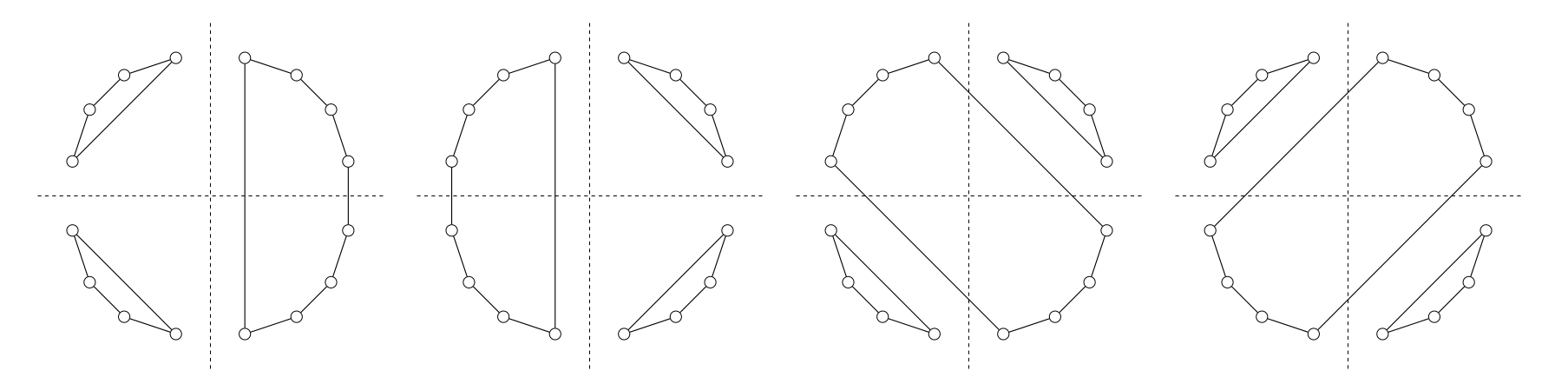
• complete: Fully connected topology where workers do AllReduce with all other workers.

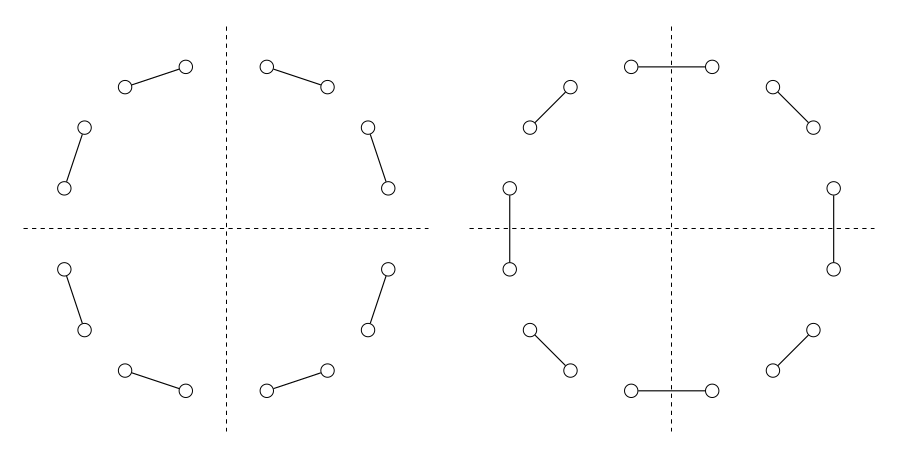
• ring: One-peer ring topology where workers do AllReduce with one of its two neighbors with adjacent ranks in each iteration.

  

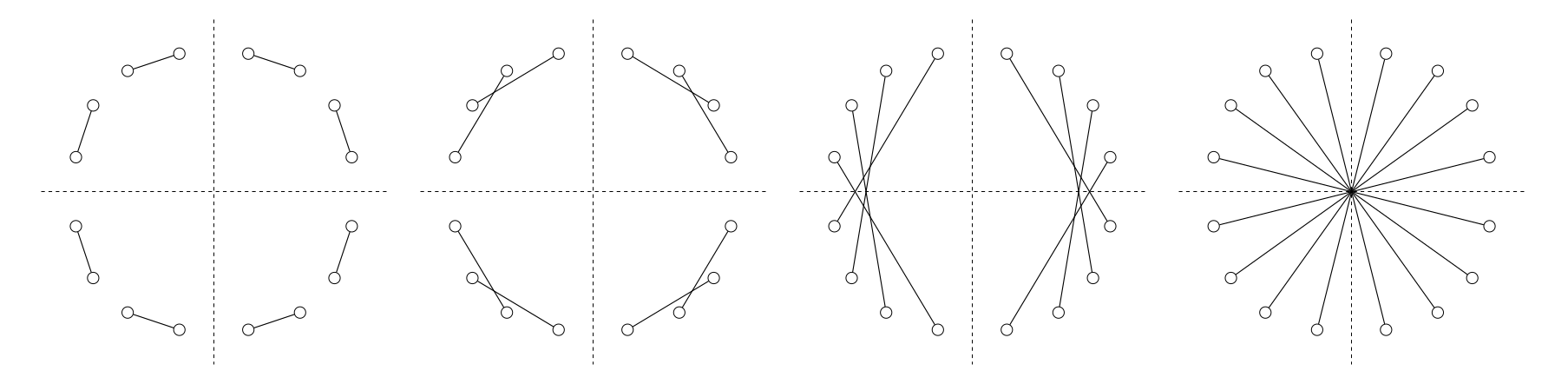
• exp: Exponential topology where worker \(i\) do AllReduce with worker \((i+2^{t \mod \log_2(n)}) \mod n\) for \(t\)-th iteration, where \(n\) is the number of workers.

  

• alternating-exp-ring: Alternating exponential ring topology (described in Figure 12 in the paper).

  

How to register a new topology

A new topology should fulfill the following requirements: - The topology should be a subclass of Topology. - The topology should implement the method: _get_topo_edges which return topology described by List[List[Edge]] which is the list of edges for each worker and for each iteration.

The Edge class is defined as follows:

@dataclass
class Edge:
    ranks: List[int]
    weight: float
    group: Optional[ProcessGroup] = None

where rank is the list of ranks of the workers involved in the communication operation, weight defines the fraction of the message that each worker keeps. For example, if the weight is 0.3, then the worker keeps 30% of its message and shares 70% with other workers.

\[x_i = w\cdot x_i + (1-w)\cdot\frac{1}{|\text{ranks}|-1}\sum_{j \in \text{ranks},j\neq i} x_j\]

where \(w\) is the weight and \(\text{ranks}\) is the ranks of the workers participating in this communication. The weight should be between 0 and 1 for convergence.

• In the topology, each worker should be involved in exactly one communication operation (or Edge).

An example of registering the ring topology is shown below:

@TopologyReg.register('ring')
class RingTopology(Topology):
    """One-peer ring topology where each node communicates with one of its left and right \
        neighbors (by index) in each iteration. The weights are 0.5 for each neighbor.
    """

    def _get_topo_edges(self) -> List[List[Edge]]:
        if self._world_size % 2 != 0:
            logger.error('Ring topology is not supported for odd world size')
            raise ValueError()

        edges = [[], []]
        # Odd iterations
        for i in range(0, self._world_size, 2):
            edges[0].append(Edge(
                ranks=sorted([i, (i + 1) % self._world_size]),
                weight=0.5
            ))
        # Even iterations
        for i in range(0, self._world_size, 2):
            edges[1].append(Edge(
                ranks=sorted([i, (i - 1 + self._world_size) % self._world_size]),
                weight=0.5
            ))
        return edges

Please refer to the decent_dp.topo module for more details.